Solitaire Auto-Solve made with Haskell

In 2013, for a university assignment in Computer Science, I developed a Solitaire (Patience) card game implementation in Haskell, a sophisticated purely functional programming language. The variant I tackled was 8-Off Solitaire.

A notable aspect of this project was creating an ‘auto-solve’ function. This advanced feature, given a deck of cards, autonomously attempts to solve the game, thoughtfully planning future moves. The code for this endeavor is available here on GitHub.

TL;DR: In the realm of Eight Off Solitaire, professional players win approximately 33.3% of their games. My Haskell-based ‘auto-solve’ implementation boasted a success rate of 29.4%, a feat I’m proud of! This assignment was awarded a first-class mark (76%).

Design

The project involved intricate design work in Haskell. Here’s a snapshot of this phase:

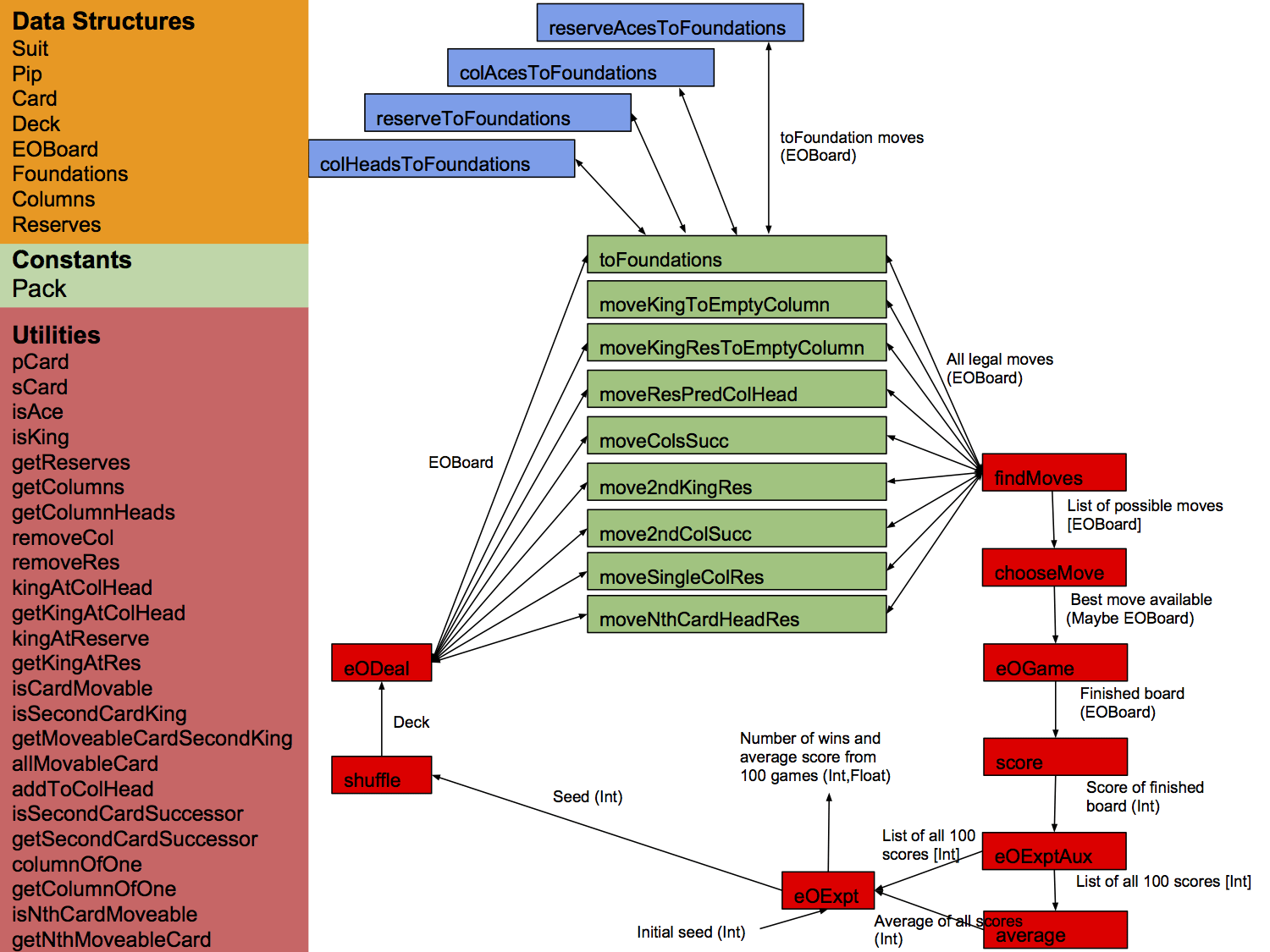
Haskell Solitaire Auto Solve Code Design

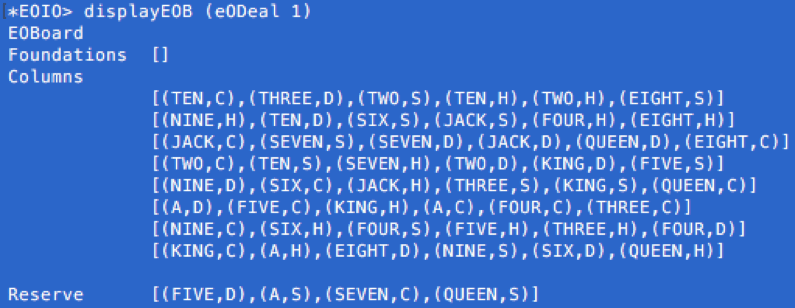
Functions and Implementation

`moveKingToEmptyColumn :: EOBoard -> EOBoard`

This function moves a King to an empty column on an EOBoard, if possible, optimizing the layout for subsequent moves.

`moveKingResToEmptyColumn :: EOBoard -> EOBoard`

It handles moving a King from the reserve to an empty column on the board.

`moveResPredColHead :: EOBoard -> EOBoard`

This function moves a reserve card to a column head if it precedes the column head card, enhancing card organization.

`moveColsSucc :: EOBoard -> EOBoard`

It rearranges columns when a card at the head of one column is a successor to the head of another column.

`move2ndKingRes :: EOBoard -> EOBoard`

This function moves the second card from the top of a column to the reserve if it’s a King, creating strategic space.

`move2ndColSucc :: EOBoard -> EOBoard`

Moves the second card in a column to the reserve if it’s a successor of another column head.

`moveSingleColRes :: EOBoard -> EOBoard`

Targets columns with a single card, moving it to the reserve if it’s not a King, thereby freeing up a column.

`findMoves :: EOBoard -> [EOBoard]`

Analyzes an EOBoard to display all possible legal moves, ranking them based on their potential effectiveness.

Haskell Solitaire Auto Solve Code Example

`chooseMove :: EOBoard -> Maybe EOBoard`

Selects the optimal move from the list generated by findMoves.

Haskell Solitaire Choose Move Function

`score :: EOBoard -> Int`

Calculates the score of an EOBoard based on the number of cards correctly placed.

`eOGame :: EOBoard -> Int`

Plays the game on a given EOBoard and returns the final score after exhausting all moves.

`eOExpt :: Int -> (Int,Float)`

Runs an experiment on the auto-solve algorithm starting from a given seed, returning the number of wins and the average score.

Experimentation and Results

Using various initial seeds for eOExpt, I conducted multiple tests to evaluate the auto-solve’s effectiveness:

Seed-Based Testing: Diverse seeds showed varying success rates, demonstrating the algorithm’s adaptability to different game setups.
Success Rate Analysis: The algorithm achieved a 29.4% win rate, nearing the performance of professional Eight Off players.

Summary

The project provided deep insights into functional programming and algorithmic efficiency in game-solving. While there’s room for strategic improvement, particularly in move optimization, the overall performance was commendable. The success rate nearly matching that of seasoned players is a testament to the algorithm’s robustness.